Referring to a one-degree square in RDF using c-squares

I'm in the midst of rebuilding iSpecies (my mash-up of Wikipedia, NCBI, GBIF, Yahoo, and Google search results) with the aim of outputting the results in RDF. The goal is to convert iSpecies from a pretty crude "on-the-fly" mash-up to a triple store where results are cached and can be queried in interesting ways. Why? Partly because I think such a triple store is an obvious way to underpin a "biodiversity hub" of the kind envisaged by PLoS (see my earlier post).

As ever, once one embarks down the RDF route (and I've been here before), one hits all the classic stumbling blocks, such as "what URI do I use for a thing?", and "what vocabulary do I use to express relationships between things?". For example, I'd like to represent the geographic distribution of a taxon as depicted on a GBIF map. How do I describe this in a RDF document?

To make this concrete, take one of my favourite animals, the New Zealand mud crab Helice crassa. Here's the GBIF map for this taxon:


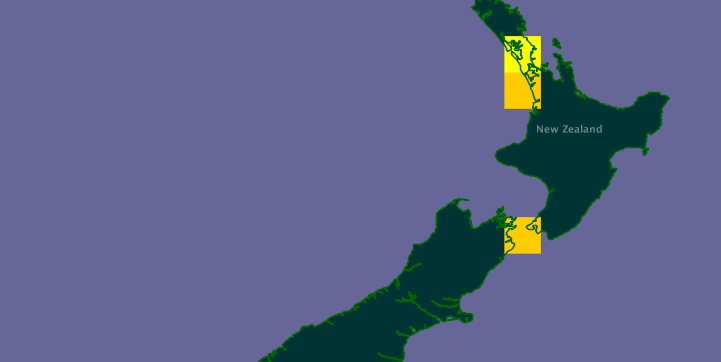
This map has the URL (I kid you not):

http://ogc.gbif.org/wms?request=GetMap
&bgcolor=0x666698
&styles=,,,
&layers=gbif:country_fill,gbif:tabDensityLayer,gbif:country_borders,gbif:country_names
&srs=EPSG:4326
&filter=()(
%3CFilter%3E
%3CPropertyIsEqualTo%3E
%3CPropertyName%3Eurl
%3C/PropertyName%3E
%3CLiteral%3E
%3C![CDATA[http%3A%2F%2Fdata.gbif.org%2Fmaplayer%2Ftaxon%2F17462693%2FtenDeg%2F-45%2F160%2F]]%3E
%3C/Literal%3E
%3C/PropertyIsEqualTo%3E
%3C/Filter%3E)()()
&width=721
&height=362
&Format=image/png
&bbox=160,-45,180,-35

(or http://bit.ly/cuTFW9, if you prefer). Now, there's no way I'm using this URL! Plus, the URL identifies an image, not the distribution.

But, if we look at the map we see that it is made of 1° × 1° squares. If each of those had a URI then I could simply list those squares as the distribution of the crab. This seems straightforward as GBIF has a service that provides these squares. For example, the URL http://data.gbif.org/species/17462693 (where 17462693 corresponds to Helice crassa) returns:

MINX	MINY	MAXX	MAXY	DENSITY
167.0	-45.0	168.0	-44.0	5
174.0	-42.0	175.0	-41.0	20
174.0	-38.0	175.0	-37.0	17
174.0	-37.0	175.0	-36.0	4

These are the 1° × 1° squares for which there are records of Helice crassa. Now, what I'd like to do is have a URI for each square, and I'd like to do this without reinventing the wheel. I've come across a URI space for points of the globe (the WGS 84 Geographic Point URI Space"), but not one for polygons. Then it dawned on me that perhaps c-squares, developed by Tony Rees at the CSIRO in Australia, would do the trick¹. To quote Tony:

C-squares is a system for storage, querying, display, and exchange of "spatial data" locations and extents in a simple, text-based, human- and machine- readable format. It uses numbered (coded) squares on the earth's surface measured in degrees (or fractions of degrees) of latitude and longitude as fundamental units of spatial information, which can then be quoted as single squares (similar to a "global postcode") in which one or more data points are located, or be built up into strings of codes to represent a wide variety of shapes and sizes of spatial data "footprints".

C-squares appeal partly (and this says nothing good about me) because they have a slightly Byzantine syntax. However, they are short, and quite easy to calculate. I'll let the reader find out the gory details. To give an example, my home town, Auckland, has latitude -36.84, longitude 174.74, which corresponds to the 1° × 1° c-square with the code 3317:364.

Now, all I need to do is convert c-squares into URIs. If you append the c-square to http://bioguid.info/csquare:, like this, http://bioguid.info/csquare:3317:364, you get a linked data-friendly URI for the c-square. In a web browser you get a simple web page like this:


A linked data client will get RDF, like this:

<?xml version="1.0" encoding="utf-8"?>
<rdf:RDF 
   xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" 
   xmlns:rdfs="http://www.w3.org/2000/01/rdf-schema#" 
   xmlns:dcterms="http://purl.org/dc/terms/" 
   xmlns:dwc="http://rs.tdwg.org/dwc/terms/" 
   xmlns:geom="http://fabl.net/vocabularies/geometry/1.1/">
   <dcterms:Location rdf:about="http://bioguid.info/csquare:3307:364">
      <rdfs:label>3307:364</rdfs:label>
      <geom:xmin>74</geom:xmin>
      <geom:ymin>-37</geom:ymin>
      <geom:xmax>75</geom:xmax>
      <geom:ymax>-36</geom:ymax>
      <dwc:footprintWKT>POLYGON((-37 75,-37 74,-36 74,-36 75,-37 75))</dwc:footprintWKT>
   </dcterms:Location>
</rdf:RDF>

Now, I can refer to each square by it's own URI. This will also enable me to query a triple store by c-square (e.g., what other taxa occur within this 1° × 1° square?).

1. Tony Rees had emailed me about this in response to a tweet about URIs for co-ordinates, but it took me a while to realise how useful c-square notation could be.